Unifoundry.com

Swedish-American civil engineer John William Nystrom (1824–1885, born Johan Vilhelm Nyström in Sweden) developed a base 16 system of counting while residing in Philadelphia, Pennsylvania. He called this new system of counting the Tonal System after his new word for 16, ton (after the English word "ten"). He greatly elaborated on his new system in 1862 in a 106-page book, Project of a New System of Arithmetic, Weight, Measure and Coins, Proposed to Be Called the Tonal System, with Sixteen to the Base. Reprints of this book are still available. This system might provide enjoyment for today's computer scientists and others who are used to working in hexadecimal.

He formulated what today would be called a base 16 (or hexadecimal) arithmetic system. The Tonal system introduced several new digits to allow each digit to represent values from 0 through 15. To differentiate them from ordinary decimal numbers, he gave these digits new names. Powers of 16 were also given new names, so as not to be confused with the tens, hundreds, thousands, etc. of decimal arithmetic.

This work was done at a time when a growing interest was developing for an international decimal system coordinated by the International Association for Obtaining a Uniform Decimal System of Weights, Measures, and Coins. John Nystrom presented his ideas to this "International Decimal Association" in England in 1859.

Counting in the Tonal System

John Nystrom gives the following pronunciation guidance for his digit names: "The names of the Tonal figures are contained in the following four words, Andetigo, Subyrame, Nikohuvy, Lapofyton, which should be learned by heart. The vowel y in these names should be pronounced as in the English word cylinder, i as in will, e as in then, a as in all." Those four words encapsulate the Tonal System digits 0x1 ("an") through 0xF ("fy"), and finally 0x10 ("ton").

His book states on p. 17 (decimal!): "The object of employing different consonants to the names of the figures is to render it more difficult to alter a written number from one value to another ; it will also make the expression clearer."

These are the 16 digit names with their glyphs:

Tonal System Digits

Unicode CSUR	Glyph	Hexadecimal	Name
U+E8E0		0x0	Noll
U+E8E1		0x1	An
U+E8E2		0x2	De
U+E8E3		0x3	Ti
U+E8E4		0x4	Go
U+E8E5		0x5	Su
U+E8E6		0x6	By
U+E8E7		0x7	Ra
U+E8E8		0x8	Me
U+E8E9		0x9	Ni
U+E8EA		0xA	Ko
U+E8EB		0xB	Hu
U+E8EC		0xC	Vy
U+E8ED		0xD	La
U+E8EE		0xE	Po
U+E8EF		0xF	Fy

These digits combine to form larger numbers with regular names following simple rules.

Counting to 100

Unicode CSUR	Glyphs	Hexadecimal	Name
U+E8E1, U+E8E0		0x10	Ton
U+E8E1, U+E8E1		0x11	Tonan
U+E8E1, U+E8E2		0x12	Tonde
U+E8E1, U+E8E3		0x13	Tonti
U+E8E1, U+E8E4		0x14	Tongo
U+E8E1, U+E8E5		0x15	Tonsu
U+E8E1, U+E8E6		0x10	Tonby
U+E8E1, U+E8E7		0x17	Tonra
U+E8E1, U+E8E8		0x18	Tonme
U+E8E1, U+E8E9		0x19	Tonni
U+E8E1, U+E8EA		0x1A	Tonko
U+E8E1, U+E8EB		0x1B	Tonhu
U+E8E1, U+E8EC		0x1C	Tonvy
U+E8E1, U+E8ED		0x1D	Tonla
U+E8E1, U+E8EE		0x1E	Tonpo
U+E8E1, U+E8EF		0x1F	Tonfy
U+E8E2, U+E8E0		0x20	Deton
U+E8E2, U+E8E1		0x21	Detonan
U+E8E2, U+E8E3		0x23	Detonti
U+E8E2, U+E8EB		0x2B	Detonhu
U+E8E2, U+E8EE		0x2E	Detonpo
U+E8E3, U+E8E0		0x30	Titon
U+E8E4, U+E8E0		0x40	Goton
U+E8E5, U+E8E0		0x50	Suton
U+E8E6, U+E8E0		0x60	Byton
U+E8E7, U+E8E0		0x70	Raton
U+E8E8, U+E8E0		0x80	Meton
U+E8E9, U+E8E0		0x90	Niton
U+E8EA, U+E8E0		0xA0	Koton
U+E8EB, U+E8E0		0xB0	Huton
U+E8EC, U+E8E0		0xC0	Vyton
U+E8ED, U+E8E0		0xD0	Laton
U+E8EE, U+E8E0		0xE0	Poton
U+E8EF, U+E8E0		0xF0	Fyton
U+E8E1, U+E8E0, U+E8E0		0x100	San

Long number names use hyphens to separate components, just as in English we say, for example, "forty-two". Long numbers can be written with commas every four digits, which is every 16 bits. These commas extend into the written names of larger numbers, as shown in the table below. Numbers 0x200 and above are the examples that appear in Nystrom's book.

Large Numbers

Glyphs	Hexadecimal	Name
	0x100	San
	0x101	Sanan
	0x106	Sanby
	0x110	Santon
	0x113	Santonti
	0x120	Sandeton
	0x12A	Sandetonko
	0x200	Desan
	0x28F	Desan-metonfy
	0x3DB	Tisan-latonhu
	0x700	Rasan
	0x1000	Mill
	0x2000	Demill
	0x8BC5	Memill-husan-vytonsu
,	0x10000	Bong
,	0xC0610	Vybong, bysanton
,	0x10 0000	Tonbong
,	0x100 0000	Sanbong
,	0x1510 0000	Mill-susanton-bong
, ,	0x1 0000 0000	Tam
, , ,	0x1 0000 0000 0000	Song
, , , ,	0x1 0000 0000 0000 0000	Tran
, ,	0x2 8D5B 7E0F	Detam, memill-lasan-suton-hubong, ramill-posanfy

Fractions

Any fraction that is a multiple of a reciprocal of a power of 2 (1/2, 3/4, 7/8, 5/16, etc.) has an exact representation in the Tonal System. Any fraction that is not is a repeating fraction. Here are some examples.

Decimal and Tonal Fractions

Decimal Fraction	Tonal Fraction
1/64 = 0.015625	/ = .
1/32 = 0.03125	/ = .
1/16 = 0.0625	/ = .
1/8 = 0.125	/ = .
1/4 = 0.25	/ = .
1/3 = 0.333…	/ = .…
25/64 = 0.380625	/ = .
1/2 = 0.5	/ = .
3/4 = 0.75	/ = .

Tonal Musical Notation

The second part of the Tonal System is a new marking for music clefs. The following table gives a summary of these new clef notations.

Tonal Music Clefs

CSUR	Glyph	Clef	Voice	Relationship
U+E8F4		Canto	Soprano	Two octaves above treble pitch.
U+E8F3		Alto	Contralto	One octave above treble pitch.
U+E8F2		Treble	Descant	Normal female voice.
U+E8F1		Tenor	Tenor	One octave below treble clef; natural voice of a man.
U+E8F0		Bass	Bass	Two octaves below treble clef; ordinary bass clef.

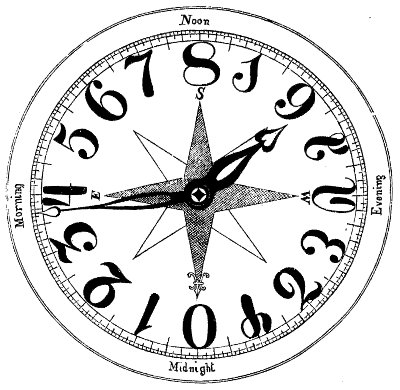
Tonal Time, Angles, and Length

To understand the note pitch indicated by the Tonal System musical notation, it is necessary to understand Tonal time. The Tonal System divides a circle into 16 parts. It applies this division to time (16 decimal hours in the day), and to longitude. This unit of division is the "tim". A circle is divided into tims (16 tims decimal). The tim is further subdivided as follows:

Tonal Time Divisions

Unit	Divisions
Circle	Tims
Tim	Timtons
Timton	Timsans
Timsan	Timmills
Timmill	Millimeter = 1.31836 seconds of time or 19.77″ of a circle

The Tonal System defines the millimeter as the length of one tinmill of time of rotation at the Earth's equator.

Angles are given as an integer followed by two Tonal digits. For example, the angle . is described as "sutim and metonby". [John Nystrom gives this example in his book on p. 33, but accidentally gives part of the number in decimal names.]

Tonal time is given as a whole number of tims, followed by a two-digit timton value. For example, the time . is "kotim and titonhu". A third hand on the dial would measure timbongs (i.e., / of a day (or 0.082 of our seconds).

The illustration below shows a Tonal clock. Midnight is at the bottom, noon is at the top.

Tonal Clock

The "natural" pitch that John Nystrom describes is (16 decimal) vibrations per tinmill on p. 33, but as. (256 decimal) vibrations per tinmill on p. 45. Of these two, the latter value is likely what he meant. With 86,400 seconds in a day, this gives 86,400 / 16⁶ ≈ 0.00514984 vibrations per second, which is a frequency of 194.18 Hz. This is approximately two semitones below 218 Hz, which is very close to concert pitch of 220 Hz for the A below middle A. (The ratio between semitones is the 12th root (decimal) of 2. On p. 47, the Tonal System gives the base pitch as 195 Hz [though 194 Hz is more accurate], approximately the pitch of F sharp.)

The Tonal System begins the natural music scale with the A note.

John Nystrom extolls the virtues of the Boehm flute as "the only wind instrument constructed on purely scientific principles, and which has attained perfection..." He mentions meeting Mr. Boehm in 1858. John Nystrom appears to have travelled far and wide in search of metrological perfection.

Tonal Money

The Tonal System also extends itself to monetary values. John Nystrom recommended dividing the dollar into 16 decimal shillings, and dividing each shilling into 16 decimal cents. Thus there would be tonal cents to the dollar (256 decimal cents) and tonal shillings to the dollar (16 decimal shillings).

Tonal coin denominations were recommended as follows:

• Copper: , , and cents.
• Silver: cents; , , , and shillings; dollar.
• Gold: , , , , , and dollars

Tonal Arithmetic Devices

The Tonal Counting Machine, shown below, is modeled after the abacus. It can expedite performing addition and subtraction using Tonal arithmetic, and even multiplication and division. It is constructed using brass wires in a square frame with tonal "balls" for counting. Line c is a "void line", meant to separate a fractional part in rows a and b from the whole part. Line h lies between mill and bong; in writing Tonal numbers, this line represents where one would place a comma.

Tonal Counting Machine (Abacus)

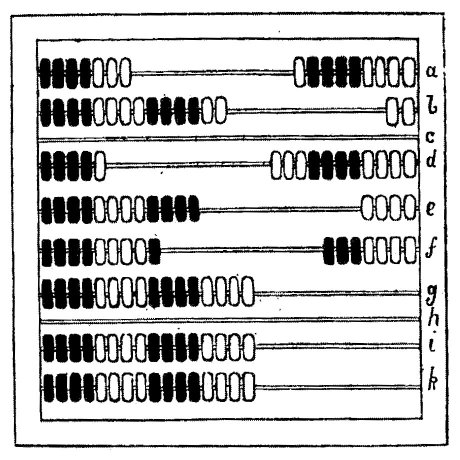
To use the Tonal Counting Machine, begin with all the balls on the left-hand side, and move balls to the right as necessary. Numbers are read from bottom to top. Thus the number displayed above (reading the balls on the right-hand side from bottom to top) is .. If used in the shop or market to tally money, this could represent dollars, shillings, and cents, with dollars on rows f through d, shillings on row b, and cents on row a.

Multiplication, Division, and Trigonometric Operations

Nystrom's calculator, shown below, facilitates multiplication and division of tonal numbers. He was awarded Patent Number 7961 (720 kB) for this device.

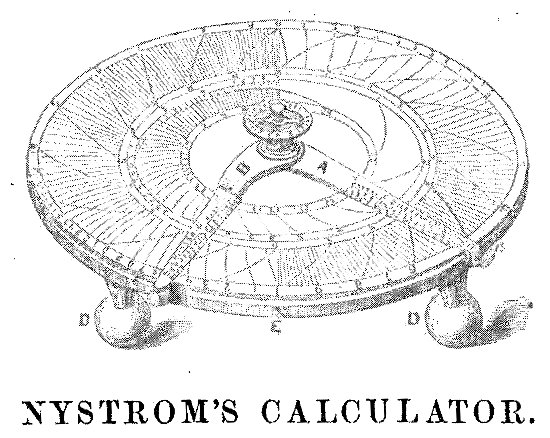
A picture of the patent model appears below (©National Museum of American History):

Quoting from Nystrom's book, p. 105: "This calculating machine consists of a silvered brass plate of about nine inches in diameter, on which are fixed two movable arms, extending from the centre to the periphery. On the plate are engraved a number of curved lines in such form and divisions that with their intersection with the arms, the most complicated calculations can be performed almost instantly.

"The arrangement for trigonometrical calculations is such that it is not necessary to notice the functions sine, cosine, tangent, &c., operating only by the angle expressed in degrees and minutes, and without any tables, which makes it so easy that any one who can read figures, will be able to solve trigonometrical questions. Any kind of calculation can be performed on this instrument, no matter how complicated it may be, whilst there is nothing intricate in its use."

To learn more on its operation, you can download the manual (20 Megabytes).

But wait! There's more!

The above descriptions of applications of the Tonal System are not exhaustive. For example, the book also goes into systems of weights and measures, and a year with 16 months. Those whose interest this page has piqued can search for the book; several sources publish it using print-on-demand.